We’ve heard of zero-sum games and positive-sum games. Similarly, there are zero-sum products and positive-sum products. One isn’t inherently better than the other, but it’s valuable to know which you’re building. If you do, you’ll have a much clearer picture of what success is and how to (and not to) go about getting it.

The terms

Let me revisit the definition of the original term first:

A zero-sum game exists when players can only gain something if the other players lose something.

The “zero-sum” comes from the idea that if you add up losses and gains across all players, it equals zero. Poker and chess are well-known zero sum games. A “parts-of-a-whole” analogy is good too, e.g. cutting pieces of a cake, where if one piece is bigger it means another is smaller. Zero-sum games are “strictly competitive.”

A positive-sum game (i.e. a non-zero sum game) exists when the sum of gains and losses can be more or less than zero. The classic example is prisoner’s dilemma, where players can work together to both achieve a better outcome, or work against each other (“betray” the other) for individual gain. Another is “the battle of the sexes” — a husband and wife want to go to different restaurants for dinner, but they’d rather give up their choice of where to dine than who they dine with, i.e. together instead of alone. They can compromise for a mutually better outcome.

So how does this relate to products? Well products don’t exist in isolation either. They exist within a category of other players, within a competitive landscape.

A zero-sum product is one that can only “win” when another product “loses” an equal amount, i.e. the sum of gains and losses is equal to zero.

A positive-sum product is one that can “win” even when another product doesn’t lose an equal amount, i.e. the sum of gains and losses is greater than zero — it’s possible to have a win-win game.

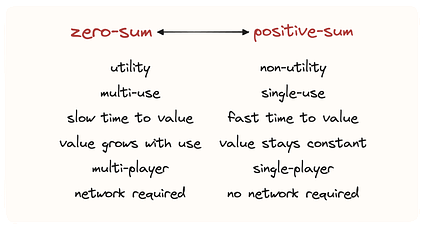
Something is either zero-sum or positive-sum, but I think it’s helpful to think about this as a spectrum of traits — products and groups of products have different characteristics that add up to being more or less zero-sum.1

Ok, so now that we’ve nailed down definitions, time to talk through some examples, a rough framework, and the decision of which kind of build.

The examples

I’ll lay out four examples that sit along this zero-sum to positive-sum spectrum.

Figma vs. Sketch

Figma and Sketch are strictly competitive, a defining feature of zero-sum products.

I really can’t be an active user of both Figma and Sketch at once. They’re pro design tools that take a while to learn how to use and you have to keep upskilling on. You store design files on them. If you have a team on it, you’re even more locked in. The switching costs are very high.

Uber vs. Lyft

These are strictly competitive too, but they have some unique properties that result in different user behavior.

I can only use one for any given trip. And when I use Uber, Lyft doesn’t get my business, and vice versa. They’re also marketplaces with powerful network effects, so one gained customer is even more valuable than the single ride they take; they indirectly add value to the overall network. (In strong network effect categories, we often hear the phrase “winner takes all”).

That said, since Uber and Lyft are very similar utilities and time to value is fast, there’s not a significant cost to bouncing between services (e.g. based on price that day). Not using Uber for a month doesn’t degrade your experience the next time either. So they’re strictly competitive, but it’s still possible for someone to be an active user of both (i.e. multi-homing) even if the usage is skewed towards one.

StarCraft vs. Dota

This example is somewhat in the middle of the spectrum — it’s not entirely zero-sum, not entirely positive-sum.

Many heavy gamers tend to have a primary game, and these large multi-player or social games do have a network effect as well. These games require significant time investment to learn and improve; and hence once you have, you might perceive a big switching cost (e.g. of time itself to learn the new game) and an opportunity cost (e.g. of not focusing on one game to improve faster).

These are both video games but different enough for someone to potentially want to learn and play both. Unlike the Uber vs. Lyft example, there is differential value offered by each unique game. And hence, they’re not strictly competitive.

Barbie vs. Oppenheimer

Pure media, especially singular products like films, are unsurprisingly not utilities. They are effectively never zero-sum products — said another way, never strictly competitive. In fact, they’re often clearly positive-sum.

Watching Barbie doesn’t really make you any less likely to watch Oppenheimer. The only real correlation could be that you don’t want to spend that much time watching movies on a given day. But that applies to movies or content broadly, not specifically Oppenheimer vs. Barbie for example. As we saw last summer, it’s possible to even bundle two movies and get people excited about a double-feature, the Barbenheimer phenomenon as we’ve come to know it.

Movies are also one-offs, they don’t require a lot of time investment (e.g. watching multiple seasons of a show), which also means it’s easy to “try” new ones. And there’s a subtle indirect network effect (e.g. you’re curious to watch things that your friends are watching), but it’s rarely core to the experience.

The Framework

It should be fairly intuitive to tease out when something is or isn’t a zero-sum product. Again, it’s not meant to be a binary designation — zero-sum or positive-sum, but more so a spectrum. Anything that’s not zero-sum is positive sum, but how positive sum?

Looking back at the examples above, there are some attributes of the products and product categories that lend to being more or less zero-sum. Consider this a rough, non-exhaustive framework to help categorize products, but notice that for any given product, not all attributes will tend to fall on one side of the spectrum!

Skeptical minds might ask, are you just talking about products being competitive with each other versus not? The answer is — kind of, but it’s more nuanced. Because not every competitive product is a strictly competitive product.

Zero-sum products are strictly competitive, which means a user ideally would only want to use one product in the category. Positive-sum products are not strictly competitive, which means a user of one product may still be interested in using a different product in the same category (even if at some level they do compete).

The Decision

So why does it matter if something is zero-sum or positive-sum?

Some of the differences are core to the business and others to the experience of the founder and team. There are intangibles here as well, like how you engage with other builders, customers, investors, and get support.

It’s significantly harder to be a new entrant in a zero-sum product category (especially the more mature it is). You have to overcome a lot to make a dent.

• When you enter the market, you’ll instantly be seen as a direct competitor. You have the burden of convincing users not just to try, but to switch.

• Intangibly, it’s harder to become friends or collaborate with other builders in the category (who are incentivized to make the category even more zero-sum).

• If you’re entering a zero-sum category as the newbie, the best bet is to go very niche in terms of the use case or customer you’re serving. This might keep the alarm bells from sounding for others in the space until you get your footing.

It’s easier to be a new entrant in a positive-sum product category, but it’s hard to carve out a unique value proposition (especially that’s durable and defensible).

• You still have the burden of getting people to try your product, but you don’t have to convince them to stop using another product at the same time.

• There’s potential to make friends and even forge partnerships with other builders in the space, and you can pitch investors who’ve invested in similar. Sometimes other products’ wins help you by increasing general awareness.

• You have more flexibility in how you enter the category; you can bill your product as “more of the same thing you like” or counter-position. And so on.

To give one last analogy, think about it this way: would you rather try to build the next YouTube or the next big YouTube channel? YouTube is the more zero-sum product and the channel on YouTube is the less zero-sum product.

Of course you’d never decide on the basis of this distinction alone, but it’s helpful to recognize when something is a zero-sum or positive-sum product, and the pros and cons that come with each. It’s certainly become a shorthand for how we talk about products in the course of building our own.

If this working theory resonates, consider scrolling up to give it a like (helps more people on Substack find it), shouting it out on socials, sharing with a friend, leaving a comment … or whatever you think is nice. 🙏

Leave a comment